看心情填坑

过了这个题一激动把耳机拉断了。。。

关于这个题的答案验证方法可见http://blog.csdn.net/lyy289065406/article/details/6648444不再赘述

但是这个做法枚举M的话基本17以上就GG了，怎么办呢

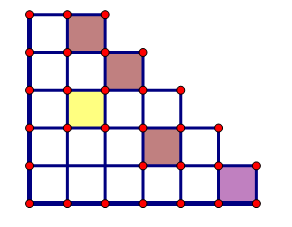
我们画个图来表示最后几次被拿掉的人的位置，左边一坨好人就不画了，右边从下到上染色的方块表示每一次被拿掉的坏人。

以n个坏人n个好人为例，我们可以知道假如第$i$行被拿掉的坏人是第$a$个坏人，和第$i+1$的方格是第$b$个坏人的话我们可以知道m=b-a(%(n+i))那么我们就可以通过BFS出所有情况然后用CRT来找出所有小于$n!$的可行解。

但是$n!$太大了_(:зゝ∠)_所以我们要找别的办法。

我们可以确定一个阈值deep,表示只考虑最后deep次的同余方程，把满足最后deep次的解求出，然后每次加上$lcm(n+1,n+2,...n+deep-1)$然后用一开始提到的方法验证。注意deep>n时答案会出错

打出表来就可以辣

另：最后一个点答案会爆unsigned long long黑人问号脸.jpg

代码里很多东西都没改，凑合着看吧，基本30以下都是秒出的，30以上要一点时间

#include<cstdio>
#include<algorithm>
#define deep 11
using namespace std;
unsigned long long heap[4000000];
long long size;
int n,cnt,cont;
bool f(int k,unsigned long long m){
    int n,i,s;
    n=2*k;s=0;
    for(i=0;i<k;i++){
        s=(m+s-1)%(n-i);
        if(s<k)return false;
    }
    return true;
}
inline int gcd(long long x,int y){return y==0?x:gcd(y,x%y);}
inline long long lcm(long long x,int y){return x*y/gcd(x,y);}
void pushdown(){
	int k=1;
	while((k<<1)<=cnt){
		int v=k<<1;
		if(v<cnt)if(heap[v|1]<heap[v])v++;
		if(heap[k]>heap[v])swap(heap[k],heap[v]);
		else break;
		k=v;
	}
}
inline long long exgcd(long long x,long long y,long long &a,long long &b){
	if(y==0){
		a=1;b=0;
		return x;
	}
	int t=exgcd(y,x%y,b,a);
	b-=x/y*a;
	return t;
}
inline long long mul(long long x,long long y,long long mo){
	long long ans=0;
	for(;y;y>>=1,x=(x+x)%mo)if(y&1)ans=(ans+x)%mo;
	return ans;
}
inline long long crt(long long mo1,long long a1,long long mo2,long long a2){
	long long a,b,t=exgcd(mo1,mo2,a,b);
	if((a2-a1)%t)return -1;
	a*=(a2-a1)/t;
	b*=(a2-a1)/t;
	b*=-1;
	long long tmp=lcm(mo1,mo2);
	return (mul(a,mo1,tmp)+a1)%tmp; 
}
void dfs(long long mo,long long k,int now,int last){
	if(now==deep){
		if(k)heap[++cnt]=k;
		else heap[++cnt]=size;
		return;
	}
	for(int i=0;i<=now;i++){
		int p=(i-last+n+now)%(n+now);
		long long t=crt(mo,k,n+now,p);
		if(t==-1)continue;
		else dfs(lcm(mo,n+now),t,now+1,i);
	}
}
int main(){
	freopen("out.txt","w",stdout);
    for(n=39;n<=40;n++){
		cnt=0;
		size=n+1;
		for(int i=2;i<deep;i++)size=lcm(size,n+i);
		dfs(n+1,0,2,0);
		dfs(n+1,1,2,1);
        fprintf(stderr,"%d %I64d\n",cnt,size);
		sort(heap+1,heap+1+cnt);
		unsigned long long ans;cont=0;
        while(1){
            if(f(n,heap[1])){ans=heap[1];break;}
            heap[1]+=size;pushdown();cont++;
            if(cont%1000000==0)fprintf(stderr,"%I64u\n",heap[1]);
        }
        printf("%I64u\n",ans);
        fprintf(stderr,"%d\n",n);
    }
}